| Unstayed Masts | Page 1 2 3 4 5 6 7 8 |
There is not a whole lot in the literature about the design of unstayed masts. Perhaps this is because, apart from rather small spars, they haven't been used so very much on yachts until fairly recent times.
This article is intended to address this lack and to provide some basic information about one way of approaching the design of unstayed spars. At the end of the article there is a reference table of all the formulae and results that are discussed throughout the article.
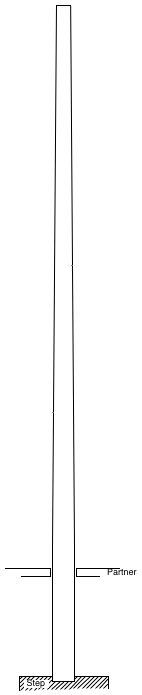 An unstayed mast (sketch on left) is essentially a very simple bit of kit. It is supported in only two places:
An unstayed mast (sketch on left) is essentially a very simple bit of kit. It is supported in only two places:
– The mast step where the heel of the mast sits, and
– The mast partner which the mast passes through at the deck.
For our purposes we can consider the the step-to-partner part of the mast as fixed and the remainder of the mast as cantilevered from the partner. If the mast breaks under the loads imposed by the sails, it is reasonable to assume that it will snap off at the partners. This allows us to consider the strength of the mast at that one point. If that is strong enough, then the rest of the mast should be OK.
Now, what are the loads imposed on the mast by the sails? We start with the stability curve of the boat. This is often called the GZ curve because it is a graph of the length of the righting arm (GZ) plotted against the heel angle. We discuss GZ and stability curves in a Stability article.
From the stability curve we can calculate the Righting Moment (RM), which is the force required to heel the vessel. Before going any further we need to be sure of our units, otherwise it is easy to get in a muddle. We use metric dimensions – lengths in metres (m), weights in kilograms (kg) and force in newtons (N). And to keep figures to readable amounts, we move to millimetres (mm) for areas and inertias.
To calculate the RM we need the displacement (∆) of the vessel in kg. Displacement is the weight of water the vessel displaces when she is floating. It is the total weight of the vessel including the ballast and everything generally on board. See here for more details. Here is the formula:
RM = GZ*∆*g g is the force due to gravity ≈ 9.81 N * is the sign for "multiplied by"
Let's put some numbers in so we can work an actual example. I will use the figures from our Design No. 152
| Displacement (∆) | 1,490 | kg |
| Maximum Righting Arm (GZmax) | 0.481 | m |
| Righting Arm at 30º (GZ30) | 0.277 | m |
From these figures we can calculate the Maximum Righting Moment (RMmax) and the Righting Moment at 30º (RM30).
RMmax = 1,490 * 0.481 * 9.81 = 7,030.729 Nm
RM30 = 1,490 * 0.277 * 9.81 = 4,048.881 Nm
RMmax occurs at about 60º on this design, which is pretty typical. So at angles of heel up to 60º the RM will be gradually increasing, reaching its maximum at 60º and then reducing again thereafter. RMmax is therefore the maximum force the sails can apply to the mast to heel the vessel, and this will heel the vessel to 60º. At any other angle of heel, RM will be less.
Just considering the force applied to the mast by the sails in order to heel the vessel we now know that at 30º it is 4,049Nm and the maximum it will ever be is 7,031Nm. The force required to heel the vessel can be considered the force required to make the vessel move forward, because the forward movement is a component of the vessels resistance to heeling. We know this in practical terms when we are sailing. A gust hits the sails and at first the boat heels sharply and then recovers as the vessel accelerates forward. We could say that the heeling force has been converted into forward motion by virtue of the vessels stability. So, basically, we have now got a handle on the force applied to the mast to make the vessel sail (a mixture of heeling and forward motion).
There are of course other forces on the mast whan sailing. The movement of the boat in a seaway for example, applies dynamic forces to the mast. These are hard to calculate and vary widely. We deal with them by applying safety factors, which have been found by experience to be suitable.
© George Whisstock. This article is for information only and may not be commercially reproduced in any form or used in any way without permission. Do not use this material as the basis for designing a mast without professional advice.
15'6" 2-berth yawl | 17'6" 3-berth yawl | 18'6" 3-berth yawl | 19' 2-berth sloop | 20' 4-berth yawl
23' chine cutter | 23' classic gaff cutter | 26' fast sloop | 30' fast cutter | 67' cruising cutter
22' cat yawl | Extended No. 119 | Commissioning a New Design |
Why wood-epoxy? | Wood-epoxy #1 | Wood-epoxy #2 | Wood-epoxy #3 | Aluminium Construction | Steel Construction
Woodbridge Poster | Rockland USA | Woodbridge UK | Whisstocks 1926-1990
Plan formats | Support | How to order | Study plans | Build plans | Designer | Kits | Laminating | Company | Privacy | Contact
Site designed, programmed and hosted by Debenriver Ltd

